Simplify Quilt Math with
the Quilter's Magic Number

This post contains affiliate links, for which I receive compensation.

The Magic Number is used for several calculations in quilting.

A case in point is Nancy's question where she inquires...

My 8" blocks will be set on point. My quilt needs to measure 100" x 110". How many blocks will I need?

I know I need triangles to fill in the spaces on the sides.

Thanks in advance for all your help!

This is a TERRIFIC question because it has several applications in quilting. On this page, we'll learn what the magic number is and how to calculate it and share an example using it to determine a quilt's size.

Allergic to math? Don't worry.

There's a free chart to download at the bottom of this page with the calculations done for you!

Calculate the width of a quilt block set on-point with the Quilter's Magic Number

The Quilter's Magic Number is...

1.414

It's calculated using the Pythagorean Theorem. Mathematicians use the theorem to describe the relationship between the hypotenuse and the two shorter sides of a right or 90° triangle.

Huh, what??!

Hy-pot-a-who???

Everyday, quilter's use it to quickly find the diagonal width of blocks and determine what size to cut setting- and corner-square triangles for on-point quilts. Knowing this one number can save you a lot of time and headache.

It's not really magic. Just math.

Now if you trust me, you can skip this next section with the light blue background—it just shows the calculations used to arrive at this number—and skip down to using it to find the diagonal length of a block.

All you really need to know for quilting is that it works!

Calculate the Magic Number
using the Pythagorean Theorem

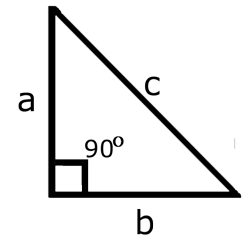
A right triangle is one that includes a 90° angle.

The short sides are labeled 'a' and 'b'. They are adjacent to each other and meet at the 90° angle.

The long side is labeled 'c'. It is opposite the 90° angle and referred to as the hypotenuse. (For us, quilters, it's the length of the diagonal of a square block.)

The Pythagorean Theorem states their relationship as...

a² + b² = c²

In plain English that means multiply the length of one short side times itself (a²). Repeat for the second short side (b²). Add those two numbers together. This sum is equal to the length of the longer side times itself or c².

All right triangles have this relationship between their sides, whether they are a half square triangles (shown above, right) or half rectangles cut diagonally from corner to corner. As long as there's a right angle between a and b, the theorem holds true, c equals the length of the diagonal.

To find c simply calculate the square root. And I say 'simply' because there's a button on your calculator to find it with a single click.

√ a² + b² = c

For a triangle with both short sides equal to 1, substitute 1 into the equation for a and b and do the math:

√ 1² + 1² = √ 2

Find the square root of 2 to determine the length of the hypotenuse or c.

√ 2 = 1.414213562373095

WHEW! That's a wicked lot of decimals!

Don't worry. For quilting, just round to three—1.414—Really. That's plenty.

This is our 'Magic Number'. It represents the ratio of the hypotenuse to the side of a square.

We can say it another way and for some it may more sense this way. Multiply our Magic Number by 100 to convert it to a percentage, like this:

1.414 x 100 = 141.4%

In plain English, the diagonal of a square, c, (the same line as the hypotenuse of our right triangle) is 141.4% of the length of a side.

Now we're cookin' with gas!

Use the Quilter's Magic Number
to find the length of the diagonal of a block

To find the diagonal measurement of Nancy's 8" finished blocks, multiply the side measurement, 8", by the Magic Number, 1.414.

8" x 1.414 = 11.312"

The width of an on-point 8" block is 11.312".

Click here to see it calculated using the formulas from above for proof that our magical Number works.

Calculate the number of blocks needed

For a patchwork design measuring 100" wide by 110" long, simply divide the finished width and length by 11.312".

100" ÷ 11.312" = 8.840 blocks wide
110" ÷ 11.312" = 9.724 blocks long

Since we don't make partial blocks, you can either round up or down to the nearest whole one, depending on your design needs.

Choose the measurement that works best for you. I've worked out the possible finished sizes in the chart below.

Rounding the # of Blocks
Dimension	Down to...	Up to...
Width	8 x 11.312" = 90.496"	9 x 11.312" = 101.808"
Length	9 x 11.312" = 101.808"	10 x 11.312" = 113.12"

At this point, to come closer to your desired finished size, you may want to audition different sashing or border alternatives.

What about rounding?

In our example, the diagonal of an 8" block is 11.312".

Since I don't do these calculations in my head, but rather on a calculator, I prefer to round only when I get to the final answer. The number is close enough for my needs.

You, however, could choose to round 11.312" either up or down to the nearest rotary cutter 'friendly' number.

For this example, that would be either 11-1/4" or 11-3/8" because it's right in the middle between 11.25 and 11.325.

Other quilting-related uses for 1.414

This magic number is also used it figure the cutting dimensions for setting- and corner-triangles for quilts set on-point as in this example.

Click here to learn more about the calculations for those units.

You can skip the math if you'd like, it's done for you at the bottom of that page!

Download the Free Cheat Sheet

Free Chart for the Dimensional Measurements of Finished Blocks

No magic needed!

Just click on the image to the right to download your free PDF cheat sheet "Diagonal Measurements of Finished Blocks".

It includes finished block sizes up through 20" square along with their diagonal measurements to three decimal places and that number rounded up to the nearest 1/8" for a rotary cutter friendly dimension.

Print and keep a copy (or two) by your sewing machine for quick access!